Ellipse Specific Fitting, RANSAC and Extracting Ellipse

Ellipse Specific Fitting, RANSAC and Extracting Ellipse

This post consists of:

1. This step consists of following tasks:
   1. Read This paper and summarize it
   2. Convert MATLAB code in fig. 7 to python and extract ellipse parameters of circle.bmp and ellipse.bmp images.
   3. Plot estimated ellipses using cv2.ellipse() method.
2. We want to find the parameters of ellipse using RANSAC algorithm. If only %40 of edges in the image belong to ellipse’s edges and we want to obtain the correct parameters with probability of 0.999, how many iterations are required?
3. Do these steps in this task:
   1. Estimates parameters of ellipse using code in task 1 on ellipse_noise.bmp image
   2. As there are points that do not belong to ellipse, RANSAC is better solution here. Implement RANSAC
   3. Draw the output on ellipse_noise.bmp image
   4. Set the probability of achieving correct parameters of ellipse to 0.99 and run algorithm for 10000 times. In how many of iterations, the estimated parameters are correct?
   5. Analyze your answer

1 This step consists of following tasks:

1. Read This paper and summarize it
2. Convert MATLAB code in fig. 7 to python and extract ellipse parameters of circle.bmp and ellipse.bmp images.
3. Plot estimated ellipses using cv2.ellipse() method.

1.A Paper Summarization

The proposed method is ellipse specified which means no matter given data, a ellipse will be output. On top of that, it is computationally cheap and robust to noises. The major reason that this approach is robust and fast is that it uses least-square transformation.

First of all, they use a distance matrix with respect to ellipse equation which is called distance_matrix:

Ellipse Equation:

Distance Matrix:

Now, the parameter a is constrained using matrix called C which is 6x6 and all these constraints are linear or C.dot(a) = 1. But in this paper, constrained a is in the way that forces the fitted model to be ellipse. 4*a*c-b**2 = 1 is the equality constraint where a.T.dot(C).dot(a) = 1.

So C is:

Based on what they have covered so far, the solution of the quadratically constrained minimization will be:

Furthermore, this system can be written as below image where lambda is Lagrange multiplier and S is D.T.dot(D):

This system can be solved using generalized eigenvectors of S.dot(a) = lambda*C.dot(a). In the end, if (lambda, u) solves S.dot(a) = lambda*C.dot(a), we have:

Then a can be obtained by a = mu*u.

1.B Direct Least Square of Fitting Ellipse Implementation and Ellipse of circle.bmp and ellipse.bmp

import numpy as np
import matplotlib.pyplot as plt
import cv2
%matplotlib inline

def direct_least_square(x, y):
    D = np.mat(np.vstack([x**2, x*y, y**2, x, y, np.ones(len(x))])).T
    S = np.dot(D.T, D)
    C = np.zeros((6, 6))
    C[0, 2] = 2
    C[1, 1] = -1
    C[2, 0] = 2
    Z = np.dot(np.linalg.inv(S), C)
    eigen_value, eigen_vec = np.linalg.eig(Z)
    eigen_value = eigen_value.reshape(1, -1)
    pos_r, pos_c = np.where(eigen_value>0 & ~np.isinf(eigen_value))
    a = eigen_vec[:, pos_c]
    return a

def ellipse_center(a):
    a = a.reshape(-1, 1)
    b,c,d,f,g,a = a[1]/2, a[2], a[3]/2, a[4]/2, a[5], a[0]
    num = b*b-a*c
    x0=(c*d-b*f)/num
    y0=(a*f-b*d)/num
    return (int(y0[0, 0])+1, int(x0[0, 0])+1)

def ellipse_angle_of_rotation(a):
    a = a.reshape(-1, 1)
    b,c,d,f,g,a = a[1]/2, a[2], a[3]/2, a[4]/2, a[5], a[0]
    return int(np.rad2deg(0.5*np.arctan(2*b/(a-c))[0, 0]))

def ellipse_axis_length(a):
    a = a.reshape(-1, 1)
    b,c,d,f,g,a = a[1]/2, a[2], a[3]/2, a[4]/2, a[5], a[0]
    up = 2*(a*f*f+c*d*d+g*b*b-2*b*d*f-a*c*g)
    down1=(b*b-a*c)*( (c-a)*np.sqrt(1+4*b*b/((a-c)*(a-c)))-(c+a))
    down2=(b*b-a*c)*( (a-c)*np.sqrt(1+4*b*b/((a-c)*(a-c)))-(c+a))
    res1=np.sqrt(up/down1)
    res2=np.sqrt(up/down2)
    return (int(res1[0,0]), int(res2[0, 0]))

# read images
circle = cv2.imread('circle.bmp', 0)
ellipse = cv2.imread('ellipse.bmp', 0)

x_circle, y_circle = circle.nonzero()
x_ellipse, y_ellipse = ellipse.nonzero()

a_circle = direct_least_square(x_circle, y_circle)
a_ellipse = direct_least_square(x_ellipse, y_ellipse)

1.C Plot Estimates

center = ellipse_center(a_circle)
axis = ellipse_axis_length(a_circle)
angle = ellipse_angle_of_rotation(a_circle)
start_angle = 0
end_angle = 360
color = 150
thickness = 1
plt.imshow(cv2.ellipse(circle, center, axis, angle, start_angle, end_angle, color, thickness))

<matplotlib.image.AxesImage at 0x1749279ac50>

center = ellipse_center(a_ellipse)
axis = ellipse_axis_length(a_ellipse)
angle = ellipse_angle_of_rotation(a_ellipse)
start_angle = 0
end_angle = 360
color = 150
thickness = 1
plt.imshow(cv2.ellipse(ellipse, center, axis, angle, start_angle, end_angle, color, thickness))

<matplotlib.image.AxesImage at 0x174927ee4a8>

2 How many Iterations for %40 Inlier Data With 0.999 Correct Estimation Probability?

w = 0.4
p = 0.999
# we need at least 6 points to estimates 6 parameters of the ellipse

k = np.log(1-p) / np.log(1-np.power(w, 6))
print('Number of needed iterations: {}'.format(int(np.ceil(k))))

Number of needed iterations: 1684

3 Do these steps in this task:

1. Estimates parameters of ellipse using code in task 1 on ellipse_noise.bmp image
2. As there are points that do not belong to ellipse, RANSAC is better solution here. Implement RANSAC
3. Draw the output on ellipse_noise.bmp image
4. Set the probability of achieving correct parameters of ellipse to 0.99 and run algorithm for 10000 times. In how many of iterations, the estimated parameters are correct?
5. Analyze your answer

3.A Estimate Ellipse on ellipse_noise.bmp Via Step 1 Code

# read images
ellipse_noise = cv2.imread('ellipse_noise.bmp', 0)
x_ellipse_noise, y_ellipse_noise = ellipse_noise.nonzero()
a_ellipse_noise = direct_least_square(x_ellipse_noise, y_ellipse_noise)

center = ellipse_center(a_ellipse_noise)
axis = ellipse_axis_length(a_ellipse_noise)
angle = ellipse_angle_of_rotation(a_ellipse_noise)
start_angle = 0
end_angle = 360
color = 150
thickness = 1
plt.imshow(cv2.ellipse(ellipse_noise, center, axis, angle, start_angle, end_angle, color, thickness))

<matplotlib.image.AxesImage at 0x17492cb6390>

3.B Implement RANSAC for Ellipse

import random

def ransac(image, max_iter, threshold=5):
    ellipse_noise = image
    data = ellipse_noise
    ics = []
    best_ic = 0
    best_model = None
    xn, yn = data.nonzero()
    nzero = [(x1,y1) for x1, y1 in zip(xn, yn)]
    for epoch in range(max_iter):
        ic = 0
        sample = random.sample(nzero, 6)
        a = direct_least_square(np.array([s[0] for s in sample]), np.array([s[1] for s in sample]))
        for x, y in sample:
            eq = np.mat(np.vstack([x**2, x*y, y**2, x, y, 1])).T
            if np.abs(np.dot(eq, a.reshape(-1,1))) <= threshold:
                ic += 1
        ics.append(ic)
        if ic > best_ic:
            best_ic = ic
            best_model = a
    return a, ics

ellipse_noise = cv2.imread('ellipse_noise.bmp', 0)
a, _ = ransac(ellipse_noise, 500, 5)

3.C Draw the Estimated Ellipse Via RANSAC

center = ellipse_center(a)
axis = ellipse_axis_length(a)
angle = ellipse_angle_of_rotation(a)
start_angle = 0
end_angle = 360
color = 150
thickness = 1
plt.imshow(cv2.ellipse(ellipse_noise, center, axis, angle, start_angle, end_angle, color, thickness))

<matplotlib.image.AxesImage at 0x1749492c2e8>

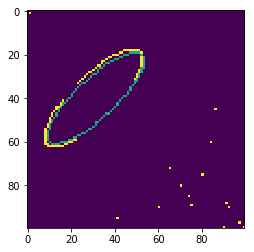
3.D If P=0.99, With 10000 Iteration, How Many Correct Estimations?

ellipse_noise = cv2.imread('ellipse_noise.bmp', 0)
a, ics = ransac(ellipse_noise, 1000, 5)

center = ellipse_center(a)
axis = ellipse_axis_length(a)
angle = ellipse_angle_of_rotation(a)
start_angle = 0
end_angle = 360
color = 150
thickness = 1
plt.imshow(cv2.ellipse(ellipse_noise, center, axis, angle, start_angle, end_angle, color, thickness))

<matplotlib.image.AxesImage at 0x17494a7e320>

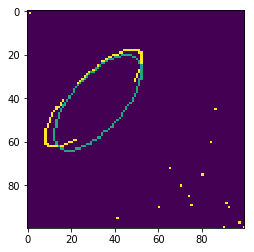
I do not know why sometimes my direct_least_square function, generates 0 parameters and sometimes 12, so the could is unstable for high number of loops. If you have any fix for this, I would be so appreciated if you could handle it using a PR! Thank you ;-)